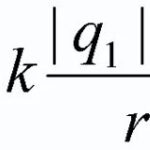Siła Lorentza i zasada lewej ręki. Ruch naładowanych cząstek w polu magnetycznym

Umieszczony w polu magnetycznym konduktorprzez który przeszedł Elektryczność, jest pod wpływem siły Ampere $FA$ , a jego wartość można obliczyć według wzoru:

$F_A=B\cdot I\cdot l\cdot grzech\alfa$ (1)

gdzie $I$ oraz $ja$ - siła prądu i długość przewodu, $B$ – indukcja pola magnetycznego, $\alfa$ - kąt między kierunkami natężenia prądu a indukcją magnetyczną. Dlaczego to się dzieje?

Siła Lorentza. Ruch naładowanej cząstki w polu magnetycznym.

Zawartość

1 Jaka jest siła Lorentza - określenie kiedy występuje, uzyskanie wzoru
2 Określanie kierunku siły Lorentza za pomocą reguły lewej ręki
3 Ruch naładowanej cząstki w polu magnetycznym
4 Zastosowanie siły Lorentza w inżynierii

Jaka jest siła Lorentza - określenie kiedy występuje, uzyskanie wzoru

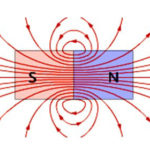
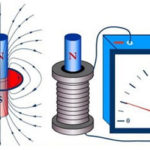
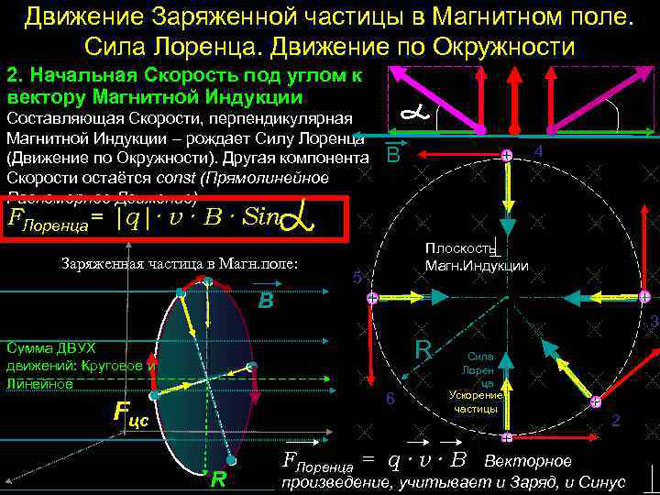
Wiadomo, że prąd elektryczny to uporządkowany ruch naładowanych cząstek. Ustalono również, że podczas ruchu w polu magnetycznym każda z tych cząstek poddawana jest działaniu siły. Aby pojawiła się siła, cząsteczka musi być w ruchu.

Siła Lorentza to siła, która działa na naładowaną elektrycznie cząsteczkę poruszającą się w polu magnetycznym.Jej kierunek jest prostopadły do płaszczyzny, na której leżą wektory prędkości cząstek i natężenia pola magnetycznego. Wypadkową sił Lorentza jest siła Ampère'a. Znając to, możemy wyprowadzić wzór na siłę Lorentza.

Czas potrzebny na przejście cząstki przez odcinek przewodnika, $t = \frac {l}{v}$ , gdzie $ja$ - długość segmentu, $v$ to prędkość cząstki. Całkowity ładunek przeniesiony w tym czasie przez przekrój przewodu, $Q = I\cdot t$ . Podstawiając tutaj wartość czasu z poprzedniego równania, otrzymujemy

$Q = \frac {I\cdot l}{v}$ (2)

W tym samym czasie $F_A=F_L\cdot N$ , gdzie $N$ to liczba cząstek w rozważanym przewodniku. W którym $N = \frac {Q}{q}$ , gdzie $q$ to ładunek jednej cząstki. Podstawianie wartości do wzoru $Q$ z (2) można uzyskać:

$N = \frac {I\cdot l}{v\cdot q}$

W ten sposób,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Używając (1), poprzednie wyrażenie można zapisać jako

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Po skurczach i transferach pojawia się wzór do obliczenia siły Lorentza

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Biorąc pod uwagę, że wzór jest napisany na moduł siły, należy go zapisać w następujący sposób:

Przeczytaj także: Jak przekonwertować ampery na waty i odwrotnie?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Ponieważ $sin\alpha = sin(180^{\circ} - \alpha)$ , następnie, aby obliczyć moduł siły Lorentza, nie ma znaczenia, dokąd skierowana jest prędkość, - w kierunku siły prądu, czy przeciwnie - i możemy powiedzieć, że $\alfa$ jest kątem utworzonym przez wektory prędkości cząstek i indukcji magnetycznej.

Zapisanie formuły w postaci wektorowej będzie wyglądać tak:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ jest iloczynem krzyżowym, którego wynikiem jest wektor o module równym $v\cdot B\cdot grzech\alfa$ .

Na podstawie wzoru (3) możemy stwierdzić, że siła Lorentza jest maksymalna w przypadku prostopadłych kierunków prądu elektrycznego i pola magnetycznego, czyli gdy $\alfa = 90^{\circ}$ i znikają, gdy są równoległe ( $\alfa = 0^{\circ}$ ).

Należy pamiętać, że w celu uzyskania poprawnej odpowiedzi ilościowej - np. przy rozwiązywaniu problemów - należy posługiwać się jednostkami układu SI, w których mierzona jest indukcja magnetyczna w teslach (1 T = 1 kg s⁻²·ALE⁻¹), siła - w Newtonach (1 N = 1 kg m/s²), natężenie prądu - w amperach, ładunek w kulombach (1 C = 1 A s), długość - w metrach, prędkość - w m / s.

Określanie kierunku siły Lorentza za pomocą reguły lewej ręki

Ponieważ w świecie makroobiektów siła Lorentza objawia się jako siła Ampère'a, do określenia jej kierunku można użyć reguły lewej ręki.

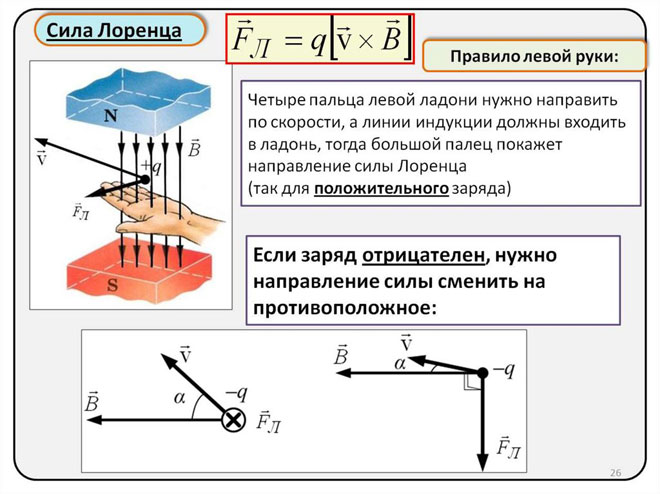
Wyznaczanie kierunku działania siły Lorentza zgodnie z regułą lewej ręki.

Należy położyć lewą rękę tak, aby otwarta dłoń była prostopadła do i w kierunku linii pola magnetycznego, cztery palce powinny być wyciągnięte w kierunku aktualnej siły, następnie siła Lorentza zostanie skierowana tam, gdzie wskazuje kciuk, co powinien być zgięty.

Ruch naładowanej cząstki w polu magnetycznym

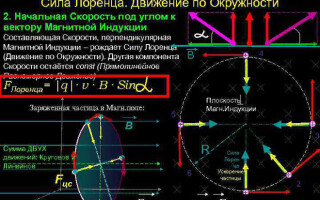
W najprostszym przypadku, to znaczy, gdy wektory indukcji magnetycznej i prędkości cząstek są ortogonalne, siła Lorentza, będąca prostopadła do wektora prędkości, może jedynie zmienić swój kierunek. Zatem wielkość prędkości i energia pozostaną niezmienione. Oznacza to, że siła Lorentza działa analogicznie do siły dośrodkowej w mechanice, a cząstka porusza się po okręgu.

Przeczytaj także: Ile watów ma kilowat?

Zgodnie z prawem Newtona II ( $F = m\cdot a$ ) możemy wyznaczyć promień obrotu cząstki:

$N = \frac {m\cdot v}{q\cdot B}$ .

Należy zauważyć, że wraz ze zmianą ładunku właściwego cząstki ( $\frac {q}{m}$ ) zmienia się również promień.

W tym przypadku okres rotacji T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Nie zależy od prędkości, co oznacza, że wzajemne położenie cząstek o różnych prędkościach pozostanie niezmienione.

Ruch naładowanej cząstki w jednorodnym polu magnetycznym.

W bardziej skomplikowanym przypadku, gdy kąt między prędkością cząstki a natężeniem pola magnetycznego jest dowolny, porusza się ona po trajektorii śrubowej - translacyjnie dzięki składowej prędkości skierowanej równolegle do pola, a po okręgu pod wpływem jego składnik prostopadły.

Zastosowanie siły Lorentza w inżynierii

Kineskop

Kineskop, który stał do niedawna, kiedy został zastąpiony przez ekran LCD (płaski), w każdym telewizorze, nie mógł działać bez siły Lorentza. Aby utworzyć raster telewizyjny na ekranie z wąskiego strumienia elektronów, stosuje się cewki odchylające, w których powstaje liniowo zmieniające się pole magnetyczne. Cewki poziome przesuwają wiązkę elektronów od lewej do prawej i cofają, cewki osobowe odpowiadają za ruch pionowy, przesuwając wiązkę biegnącą poziomo od góry do dołu. Ta sama zasada jest stosowana w oscyloskopy - urządzenia służące do badania przemiennego napięcia elektrycznego.

spektrograf masowy

Spektrograf masowy to urządzenie, które wykorzystuje zależność promienia rotacji naładowanej cząstki od jej ładunku właściwego. Zasada jego działania jest następująca:

Źródło naładowanych cząstek, które nabierają prędkości za pomocą sztucznie wytworzonego pola elektrycznego, umieszcza się w komorze próżniowej, aby wykluczyć wpływ cząsteczek powietrza. Cząsteczki wylatują ze źródła i po przejściu łuku koła uderzają w kliszę fotograficzną, pozostawiając na niej ślady. W zależności od konkretnego ładunku zmienia się promień trajektorii, a tym samym punkt uderzenia. Promień ten jest łatwy do zmierzenia i znając go, można obliczyć masę cząstki. Na przykład za pomocą spektrografu masowego zbadano skład gleby księżycowej.

Przeczytaj także: Jakie są zawody związane z elektrycznością

Cyklotron

Niezależność okresu, a co za tym idzie częstotliwości rotacji naładowanej cząstki od jej prędkości w obecności pola magnetycznego, jest wykorzystywana w urządzeniu zwanym cyklotronem i przeznaczonym do przyspieszania cząstek do dużych prędkości. Cyklotron to dwa puste w środku metalowe półcylindry - dwójka (kształtem każdy z nich przypomina łacińską literę D) umieszczone prostymi bokami do siebie w niewielkiej odległości.

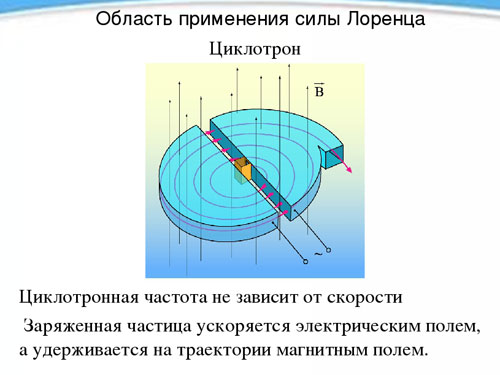
Cyklotron - zastosowanie siły Lorentza.

Dees są umieszczane w stałym jednorodnym polu magnetycznym, a między nimi powstaje przemienne pole elektryczne, którego częstotliwość jest równa częstotliwości obrotu cząstki, określonej przez natężenie pola magnetycznego i ładunek właściwy. Dostając się dwukrotnie w okresie rotacji (podczas przejścia z jednego dud do drugiego) pod wpływem pola elektrycznego, cząstka za każdym razem przyspiesza, zwiększając promień trajektorii, aw pewnym momencie osiągając pożądaną prędkość, wylatuje z urządzenia przez otwór. W ten sposób proton może zostać przyspieszony do energii 20 MeV (megaelektronowolt).

Magnetostrykcja

Urządzenie zwane magnetronem, które jest zainstalowane w każdym kuchenka mikrofalowa, to kolejny przedstawiciel urządzeń wykorzystujących siłę Lorentza. Magnetron służy do wytworzenia silnego pola mikrofalowego, które ogrzewa wewnętrzną objętość piekarnika, w której umieszcza się żywność. Zawarte w jego składzie magnesy korygują trajektorię ruchu elektronów wewnątrz urządzenia.

Pole magnetyczne Ziemi

A w naturze siła Lorentza odgrywa niezwykle ważną rolę dla ludzkości. Jego obecność pozwala ziemskiemu polu magnetycznemu chronić ludzi przed śmiercionośnym promieniowaniem jonizującym kosmosu. Pole nie pozwala na bombardowanie naładowanych cząstek powierzchni planety, zmuszając je do zmiany kierunku.

Podobne artykuły: